The Raft Spin

After the rotation fixes, one weird issue remained with Guybrush, when getting on the raft in the set mot. When Guybrush got on the raft, he would strangely rotate in a circular motion once on the raft.

To debug the problem, I commented out the lines in the set file mot.lua regarding guybrush getting on the raft and found that it was a call to setrot which caused the issue to occur. In this call, setrot was called with TRUE as the fourth parameter, causing Guybrush to rotate over time instead of snapping to the rotation. Due to some difficulties with getting the rotation before Guybrush turned out of the retail version, I used a textObject in the lua script before setrot was called to display the values. Here's the retail version and ResidualVM:

Guybrush's rotation before getting on the raft in the Retail Version

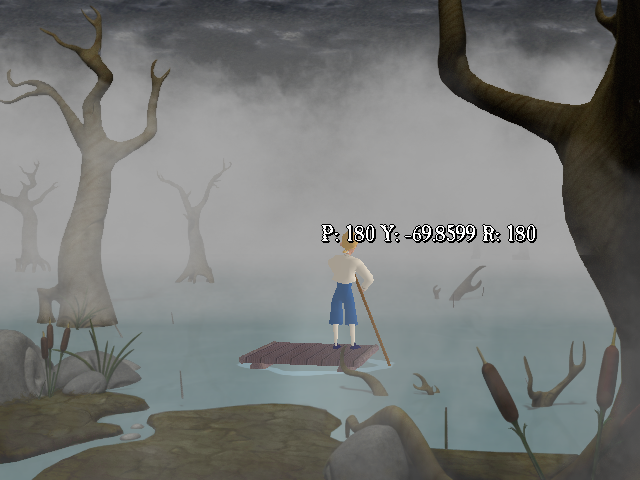Guybrush's rotation before getting on the raft in ResidualVM

As can be seen, the yaw parameter is inverted! So, is this the issue that's causing the weird rotation? I tried setting Guybrush's rotation before calling setrot(0, 0, 0, TRUE) with guybrush:setrot(180, 69.8599, 180) and found that the weird rotation still occurred. So, it seems there are actually two problems here:

1. When rotating, Guybrush is sometimes rotated in axes that he shouldn't be when setrot is called without snapping to the new angles
2. Guybrush's rotation is incorrect, with the yaw axis returning a negative value when it should be positive

To inspect the first problem, I tried setting Guybrush's rotation to 0 in each of the axes independently and inspecting the result and found that no axis was directly responsible for this rotation. I then tried setting them all to 0 with a snap and found that this looked correct (which was expected, obviously). The next experiment was to set each of the angles to a part of the rotation. I tried (0, 69.8599, 0) first and found that the result looked right, indicating that the pitch and roll axes might be causing the problem. I then tried (45, 69.8599, 45) and found that it also looked correct! However, at (90, 69.8599, 90), the issue re-appeared. In fact, any value below 90 seemed to work okay, while values greater than 90 caused problems. Out of curiosity, I then tried (-45, 69.8599, -45) and found that it also worked fine! In fact, values between -90 and 90 (non-inclusive) seemed to produce the correct result, while values outside that range produced incorrect behavior.

This pointed to a problem with the conversions between Euler angles and other rotation forms in that angles between (-90, 90) were calculated correctly, but larger angles were not. First, I checked the functions that I wrote by implementing a simple perl program to compute the rotation matrices from Euler Angles and back again. This program can be found here and produces results demonstrating the correct equations for setting a rotation matrix from Euler Angles and retrieving the Euler Angles from the matrix:

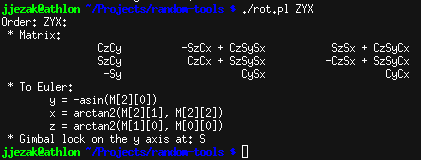Output from computing the Euler -> Matrix conversion for ZYX

Fortunately (or unfortunately for finding the bug!) the results matched and there wasn't an obvious problem, aside from the absence of checking for singularities or gimbal lock checking. However, I was having trouble keeping the X's for the axis and the X's for the Euler Angles straight, so as a part of this work, I reworked the Euler Angle nomenclature to make the naming more consistent with the usage.

With the nomenclature straightened out, I then added a fix for singularities that arise from when it's impossible to determine the correct result. For an Euler Order of ZYX, we can see that when the Y Euler Angle is pi/2 (or 90 degrees), it will be impossible to differentiate the other two angles. We can see this by inspecting the figure above, where we can see that if the result of Cy is 0, then the components that are used by the arctan cannot be used to determine the result.  Cy is 0 when the cosine of the Y axis angle is pi/2 or -pi/2. This state results in a condition called gimbal lock. To work around this issue, we can check to see if the conversion will produce gimbal lock and if so, chose a single rotation.

So, does correcting for gimbal lock fix any of our problems? We can be fairly certain that it won't just by inspection. In the scenario above, Guybrush's coordinates would not cause a singularity because the second angle (yaw) is not +/- 90 degrees. Still, it was a necessary fix!

So, what is really going wrong here? Let's try some more experimentation! First, let's rotate Guybrush from (0,0,0) to (180, 0, 0) and (0,0,0) to (0, 0, 180):

Pitch 180 Degrees - (0,0,0) to (180, 0, 0)

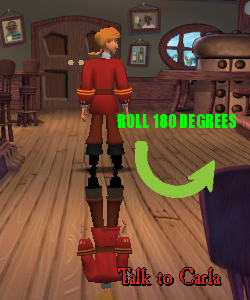Roll 180 Degrees - (0,0,0) to (0, 0, 180)

Rotation of (0,0,0) to (180, 0, 180)

We can see that the sum of these rotations is going to result in Guybrush facing 180 degrees opposite his position on the yaw axis from the (0,0,0) rotation. So, we can see that a rotation from (180, 0, 180) to (0, 0, 0) should only produce rotation in the yaw axis instead of rotating through the pitch and roll axes as well.

What causes this extra rotation? In ResidualVM, the turn methods of the Actor use Euler Angles to compute the rotation by making the angles equal. If instead, a Quaternion is used for rotation, this problem should be resolved. Now that the problem has been identified, in the next post, I'll address the issue.

What's up with Timmy?

Continued from the previous entry

In the previous entry, we started debugging the issues with the lava puzzle and found a problem with Guybrush colliding with the logs. We also found that a similar problem was occurring with the monkey Timmy, on the beach at Monkey Island. In this post, we'll try to figure out why Timmy isn't colliding with Guybrush and just running right through him instead.

Timmy on the Beach, Running Wild!

To begin with, I examined the script that controlled Timmy's running behavior. When an actor has a monkey that's running around the actor's position, a variable named monkey_range is set, which describes the maximum distance that the monkey can run from the actor in each direction. A random value within this range is chosen for the monkey to go to. The monkey runs to this location using the runto method, which is implemented by the Lua command WalkActorTo, which ultimately runs the Actor::walkTo method in ResidualVM. Within this method, the actor checks for collisions while plotting the path.

So, why isn't Timmy colliding with Guybrush? If we comment the check to print out when actors are checked for collision, we find that we can make Timmy collide with Guybrush if Guybrush walks into him, but not if Timmy runs into Guybrush when Guybrush isn't moving. If we inspect the logic that makes Timmy move, we find that there's a method in the Actor class called updateWalk which updates the character's position over the duration of the walk. If we add some code here to force a collision check when the actor is moving, Timmy stops as expected when he runs into Guybrush.

I suspect that this fixes the lava puzzle collisions too, but currently the logs in the puzzle aren't showing. I'll tackle this in the next post! This work is submitted as PR #1050.

TinyGL and the Font Segfault

With the integrations of my text patches, the text rendering is much closer to the original version. Unfortunately, it was found that they also caused memory corruption, resulting in segfaults when using the TinyGL rendering path.

First, I wasn't sure exactly what was causing the segfaults, just that they were happening at seemingly random intervals and that the backtrace usually involved a text function such as drawing or freeing a text object. I put the game into gdb and found that I couldn't reliably trigger the bug to investigate the problem. I then tried running ResidualVM in valgrind and found that when creating the text object with the function createTextObject in the TinyGL rendering path, when creating the text bitmap, there was a buffer overrun. To be sure, I added an assertion to this path that asserted when the bitmap offset was larger than the bitmap storage. This confirmed the issue!

So, what changed to cause the bitmap size to be smaller than expected? If we look at the code, it appears that the TinyGL engine is allocating the text object bitmap using the kerned height and width. As it turns out, this isn't actually enough space to hold the completed text because there's an additional piece of information, the column offset. When a letter is printed without using the whole kerned space (as in the character "1"), there's an offset added to the starting column to account for this, letting the game use less storage for the character. When I accounted for this extra width, along with adding a new function to take the y offset into consideration as well, the segfault was fixed and text was rendered properly in TinyGL again! This was submitted in PR #1024.

Simplifying Attaching and Detaching

Continued from the previous entry.

After all of the previous work on attaching and detaching and getting it pretty close to working, I found that there were still a few issues, like the cuffs not attaching properly to Guybrush's wrists in the set wed. Additionally, after a code review by Akz, he suggested that the code could be made simpler and that instead of trying to match the internal matrices in the retail version, I should just aim to match the output. Of note was that I needed to insert a large number of transposes to make the intermediate values work.

As such, I scrapped the previous code and instead tried to fix the problem of attaching and detaching with all of the new information that I'd learned over the course of debugging this problem. This new version of the attach and detach code is much less intrusive and achieves the same result with far fewer calculations. This code was re-submitted as PR #948. So, how does the pole in the set pph look now?

The set pph after getting off the raft

Looks pretty close, the pole is in the right position, but let's compare it with the original:

Difference between retail and ResidualVM

It's a little hard to see, but there's still a different in the orientation of the pole. I'm not exactly sure where this comes from, but I suspect that it has to do with the joint rotation of Guybrush's hand. Still, the result is much better than it was before.

The next outstanding rotation issue that needed to be looked into was Issue #958. I thought that I had fixed this bug, but it appears to still be broken. The best item for displaying the issue is the itty-bitty brass screw, which is rotating on the wrong axis.

Retail

ResidualVM

As you can see, the screw starts in the wrong orientation and is upside down! Additionally, the rotation of some items in the inventory are incorrect with rotation being applied to the wrong axis. As it turns out, the orientation was incorrect because the rotation was applied backwards. Inverting the rotation Quaternion result of GetRotationQuat made this problem go away, but the resulting angle was wrong for the attached actor. This was because GetRotationQuat was being used as part of the attach and detach sequence. Iverting those usages as well found that the result now matched what we had before, except that the screw was rotated correctly.

The pole in the set pph is effected by the rotation of the hand joint in Guybrush's hand. As it turns out, the code that I had written for the attach and detach had neglected the position of the attached joint. Incorporating this rotation and translation slightly improved the position and rotation of the pole in the set mot.

At this point, I was hoping that all of the issues were resolved enough to move on, but two major issues remain:

1. The boats in the lava puzzle were placed incorrectly, appearing (well, not actually appearing) under the lava instead of on top.
2. When Guybrush rotates on the raft after boarding, he spins on a wrong axis.

In the next post, we'll tackle these issues!

Working on the Remaining Issues for Text Rendering

Continued from the previous entry.

In the previous entry, we (mostly) fixed all of the text problems in the set wed, but discovered that there were issues in the set gmi. Since both Elaine and Guybrush's text were in the wrong place, I decided to make the game draw her bounding box too. Here's a typical scene with some text:

Bounding boxes drawn for Elaine and Guybrush

We can see here that the bounding box for Elaine is very wrong, while Guybrush's looks pretty good. So, there appear to be two more issues related to text positioning here:

1. The bounding boxes are still wrong
2. The text isn't being placed in the right position above the bounding box

We'll investigate each issue, starting with the bounding boxes. First, how are the bounding boxes calculated? In the graphics driver, there is a function that iterates through the transformed and projected vertices in each component of a costume and finds the bounding box coordinates that enclose these points. To debug this issue, I stepped through each costume component and tried using that as the bounding box coordinates. It turns out that using only the active costume as specified by the wearChore for the dimensions of the bounding box makes the bounding box fit the actor. The result of this change (in PR #976) is shown below:

With the new Bounding Box code

I then decided that the reposition function seemed like a hack, so I examined the retail version in a debugger and found that a simple manipulation of the X and Y coordinates produced just about the same result. With this function removed and the code simplified, here's the current output difference for this text in the set gmi:

Pretty close!

We're very close now with the text placement in this scene, with the text still being placed one pixel too low, but otherwise perfect! Let's check out some other, previously problematic scenes, starting with the set mel, when you meet Carla and Otis again for the first time:

Retail

ResidualVM

As you can see, the text placement for both characters is a little bit off. After some inspection, I found that Carla's text is placed using a specified X and Y coordinate passed as a parameter to SayLine. This text is placed by ResidualVM 9 pixels too high, as compared to the retail version. It turns out that in ResidualVM, there was code that shifted the text when it was too close to the edge, which was using a constant value for shift amount. Replacing this constant with the text height puts Carla's text 1 pixel too low, like most of the other text so far, but very close to the right position.

For Otis' text, the positioning is much further off. His text is placed 41 pixels too low and 17 pixels to the right. After some work with the debugger, I found that the Retail version of EMI was placing Otis' "Yeeps!" at the position: (394, 25). To check that this was accurate, I checked the screen  shot above and found that location, and measured to make sure that the output made sense with these numbers:

Yeeps!

So, the location matches, with the red dot in the middle of the second "e" representing the point specified by the retail version (394, 25). We can see that this dot is 25px from the top and 394 pixels to the right. We can also see that the text is centered in the X axis around this point. ResidualVM does center the text properly, but the point selected is (411, 66). So, where does the difference come from? I continued debugging until I found the bounding box information for Otis and added that to the image below, along with the "Yeeps!" text from the retail version:

Retail bounding box in red, ResidualVM in blue (center line drawn as well)

So, my previous fixes for the bounding box above didn't match the retail version, and we can see that the retail text is placed centered at the top of the retail bounding box. The retail version calculates a bounding box at point (394, 25) with a size of (254, 365).

After some discussion with Akz and Klusark on IRC and some test code, Akz saw that the retail version's bounding box could be computed from the coordinates provided as part of the costume data. Using the bounding box position as the center and projecting the points of the bounding box into screen coordinates resulted in a bounding box that matched the retail version. With this change, the text is now rendering in the right place, although it's still 1 pixel lower than it should be. Here's the difference in the scene again with Otis and Carla:

The text is pretty close now!

Another issue arose when Klusark tested the set tri. In this set, the text was layered on top of other text, resulting in a mess! This was actually the original bug that inspired all of the text refactoring in the first place, so I probably should have tested this sooner. Why wasn't this text fixed by these changes? It turns out that the text is placed based on the position of the ship. So, when the ship moves, the text should be placed relative to the ship's location. To find the ship's location, a function called WorldToScreen is called to find the screen coordinates for the ship. The text is then rendered using these coordinates. In the retail version, instead of passing a screen coordinate (0,0 -> 640,480), it instead passes a floating point value in the range -1 to 1. Removing the conversion from the function and adding it as needed throughout the graphics primitive drawing code fixes the issue, although the result isn't exactly right, with the text being drawn above the ship rather than below. Still, it's quite a bit better than it was!

Working text on the Tri-Island Map

This work can be found in the updated PR #964.

Endianness Fixes

I had some time this weekend where I wasn't at home able to work on ResidualVM. This provided an excellent opportunity to take a look at some of the issues that ResidualVM has on big-endian architectures like my PowerBook G4. I'm currently running Gentoo Linux on my Powerbook, and was able to play other OpenGL games without issue and Grim appears to work fairly well in ResidualVM. However, EMI is a mess!

The LucasArts intro has the wrong colors!

Even worse, the set wed has incorrect colors and alpha channel issues!

As can be seen above, the colors for many objects appear to be swapped from the intended colors. Let's investigate these issues, starting with the intro screen.

When debugging graphics issues like the intro screen, I often examine the colors between the working, little-endian version big-endian version to see if there the colors are easily identified as being swapped. Unfortunately, this wasn't immediately obvious as being the case. The colors were completely different:

No direct byte swap will make the right turn into the left...

However, I then checked and found that when loading bitmaps, two formats are present in ResidualVM, a packed 1555 format and a 32 bit format. With this information, it seems that the data was specifying an alpha channel, which was modifying the color components that were swapped. After some experimentation, I found that the native endianness is the preferred byte order for the Escape from Monkey Island binary format containing a bitmap image, a .til file. This worked well for 32-bit .til files, as found in the Windows version of EMI. However, the PS2 version uses 16-bit .til files. I found that it was easiest to convert the 16-bit input to a 32-bit output and doing the bit manipulation when the image was loaded.

With the .til files fixed and the intro displaying the correct colors, let's re-examine the set wed, to see if that was effected by the change:

That's a whole lot better!

While the output is now a whole lot closer, there's still a bunch of issues to be addressed. Let's focus on the background first. In the background, the enemy pirate ship is bouncing in the waves. This effect is actually achieved by an Actor object rotating and moving up and down on a timer. The Actor is drawn with a Sprite object, which are drawn using an image from a .tga file. After some inspection, I found that the desired behavior is to again read from the file in the native format. Another tweak was required to change the display format from BGR to RGB and this problem was solved. Here's the output now:

Getting closer!

Of note, this change also fixed the backgrounds for dialog boxes and other components that use .tga files. The next most obvious issue is that Guybrush and the brazier are both rendered as completely black with no color for the textures. I noticed that in the Act 1 title card, the actors were actually visible, although dim. This gave me the hunch that the lighting was to blame for the dark actors. To test this, I tried commenting out the lighting code when drawing the actor and found that the texture was drawn mostly correctly, albeit without lighting:

With lighting commented out

I then inspected the values used to dim Guybrush and found that the in the lighting object, the x, y, and z values were all NaN, causing the output to be black. As most endian issues appear when using data from the other endian systems, I looked at the loadBinary method for lighting and found that the floats used by the lighting were read in directly, rather than being interpreted by get_float() which performs the endian swap if needed. After adjusting both the Light and Shadow loadBinary methods, I got the correct output for the set wed as seen below:

Looks like it's all working correctly now!

The only outstanding issue right now on big-endian machines is that the 1555 ARGB color for the video frame isn't unpacked correctly. I suspect that an approach similar to how I fixed the 16 bit .tga files would work here as well, but I need to see if there's a better way to do this first. This work is in PR #974.

More on Text Positioning

Continued from the previous entry.

Let's take stock of the current state of the text positioning changes after the last blog post. First, let's look at the differences in the set wed when Guybrush says "There's an enemy pirate fighting over there.":

State of the text difference at the start of this post in the set wed

With the changes from before, we can see that there is less difference than when we started, but that the text for Guybrush's speech bubble is positioned to the right by 1 pixel and towards the bottom by 5 pixels. Likewise, the text for "Look at enemy pirate" is closer, but still not quite right. It appears to be 11 pixels too high, towards the top compared to the retail version.

Another place with a similar issue is the text at the top of the inventory. It appears that the text is drawn 12 pixels too high, resulting in this difference:

 Misplaced Inventory text

As an aside, the differences in object rotation in the inventory appear to be related to be related to the rotation and attachment work I've been blogging about. That work wasn't in this branch when I took the screen shot!

Anyway, there's definitely a problem with the placement of text on the Y axis, with a similar problem displayed in both sets. As it turns out, there's code that specifically moves the text in the Y direction by 12 pixels in ResidualVM. This code is found in textobject.cpp and appears to have been added with this commit. Commenting out this adjustment results in the text for the inventory being placed in the correct location and bringing the command line in the set wed within 1 pixel of the correct location. Let's take a new screen shot with this change:

Current text difference at this point

As can be seen, the action sentence at the bottom is very nearly correct and only off by one pixel. However, the speech bubble got worse. Now, the ResidualVM text is still 1 pixel to the right, but 17 pixels lower than it should be.

My first thought was that there was simply a blank line inserted below the text, but the font height for EMI was 26 pixels, not 17. I next checked the bounding boxes for the actors to see if they made sense by drawing a green line around Guybrush representing the bounding box whenever he spoke. Here's what the output of that was:

Guybrush's bounding box

However, in order to get the bounding box to draw properly, I had to subtract the Y components from 480. In order to make the code simpler, I removed the subtraction from the Y component when computing the bounding box from the bounding box calculation and re-ran the test. Here's the result after modifying the bounding box code:

The green line is the bounding box for Guybrush's actor

Although the bounding box looks a little worse (see: Guybrush's feet and hair), I checked the text position with this new bounding box and found that it was off by 26 pixels, which if you remember, was the height of the font. Subtracting 1 from the number of lines that the text was pushed up by gets the fonts for this scene rendered very closely to the original:

Very close now!

We can see that the fonts are still off by 1, but for now, this is close enough! So, let's check to see if there are problems in other scenes. Unfortunately, there are:

The text is in the wrong place again!

Here, you can see that Guybrush's speech is rendered at the wrong place in the set gmi.

As a check, I also tried this branch with Grim Fandango and found that it too had fonts drawn too low, with text 13 pixels too low and offset by 2 pixels to the right for the top line and 1 for the bottom line:

Grim also has differences in the font location

As an aside, bgK also tested this with the French version of Grim, which was reported to be problematic with using the kerned font sizes. I'm happy to say that the crashing issues from that appear to be resolved!

In the next blog post, we'll take a look at these two issues and see if we can resolve them.